看到论坛同学实现了shader方向的内容, 也找了两个觉得好看的实现了一下.
Seascape: Shader - Shadertoy BETA (但是这个FPS一直跑不高…)
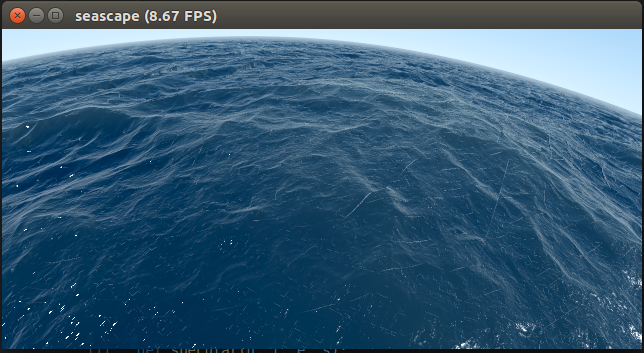
不得不说 最外层 for-loop 的 automatically parallelized 确实很利于shader的模式:D
代码在个人仓库, 欢迎交流~~
很赞呀！！早上睡眼惺忪被你的效果吓醒了，哈哈 
1 个赞
老师早上好~~送您一个爱心
Heart-2D:
(仓库代码已更新:D)
2 个赞
SeaScape
curvatic Empire2
2 个赞
补充两个新的实现 (仓库代码均已更新)
BlackHoleRayMarcing 同样来自 Shader - Shadertoy BETA
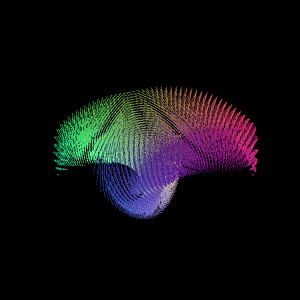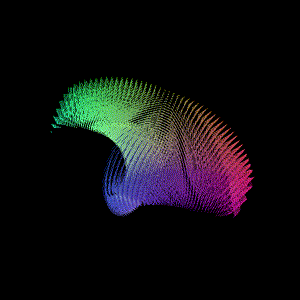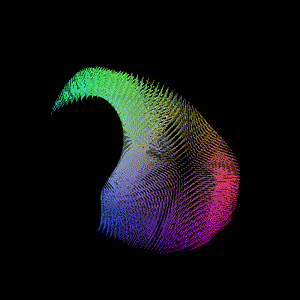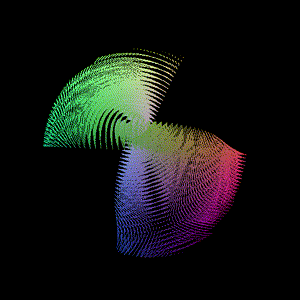
另一个是最近在看Lie Group和Lie Algebra相关内容, 可视化了SO(3)李群的李代数空间点阵
可以修改输入的欧拉角约束范围, 将对应旋转转为旋转向量(轴角)
import taichi as ti
import numpy as np
ti.init(debug=False, arch=ti.gpu)
RES = 512
K = ti.Matrix([[RES, 0.0, 0.5 * RES], [0.0, RES, 0.5 * RES], [0.0, 0.0, 1.0]]) # fov = atan2(1, 2), i.e. arctan(0.5)
PI = float(np.pi)
t_pushed = 3.0 * PI
t_farest = t_pushed + 2.0 * PI
nmax = 50 # 400
nx, ny, nz = nmax, nmax, nmax
z_buff = ti.Vector(4, dt=ti.f32, shape=(RES, RES)) # z_buffer: [r,g,b,depth]
axis_angle = ti.Vector(3, dt=ti.f32, shape=(nx, ny, nz)) # axis: [x,y,z]
aa_colormp = ti.Vector(4, dt=ti.f32, shape=(nx, ny, nz)) # cm: [r,g,b,depth]
aa_transfm = ti.Vector(2, dt=ti.i32, shape=(nx, ny, nz)) # px: [x,y]
@ti.func
def colormap(aa):
return aa / (2.0 * PI) + 0.5
@ti.func
def mix(x, y, a):
return x * (1.0 - a) + y * a
@ti.func
def euler2rotmat(rx, ry, rz):
# assume euler-order: 'rpy', roll(Z)->pitch(X)->yaw(Y)
# i.e. X => pitch, Y => yaw, Z => roll
cx, cy, cz = ti.cos(rx), ti.cos(ry), ti.cos(rz)
sx, sy, sz = ti.sin(rx), ti.sin(ry), ti.sin(rz)
m00 = cx * cz + sx * sy * sz
m01 = cz * sx * sy - cx * sz
m02 = cy * sx
m10 = cy * sz
m11 = cy * cz
m12 = -sy
m20 = cx * sy * sz - sx * cz
m21 = sx * sz + cx * cz * sy
m22 = cx * cy
return ti.Matrix([[m00, m01, m02], [m10, m11, m12], [m20, m21, m22]])
@ti.func
def rotmat2quaternion(rotmat):
m00, m01, m02 = rotmat[0, 0], rotmat[0, 1], rotmat[0, 2]
m10, m11, m12 = rotmat[1, 0], rotmat[1, 1], rotmat[1, 2]
m20, m21, m22 = rotmat[2, 0], rotmat[2, 1], rotmat[2, 2]
tr = m00 + m11 + m22 # ti.tr(rotmat)
qw = ti.sqrt(1.0 + tr) / 2.0
qx = (m21 - m12) / (4.0 * qw)
qy = (m02 - m20) / (4.0 * qw)
qz = (m10 - m01) / (4.0 * qw)
return ti.Vector([qw, qx, qy, qz])
@ti.func
def rotmat2rotvec(rotmat):
m00, m01, m02 = rotmat[0, 0], rotmat[0, 1], rotmat[0, 2]
m10, m11, m12 = rotmat[1, 0], rotmat[1, 1], rotmat[1, 2]
m20, m21, m22 = rotmat[2, 0], rotmat[2, 1], rotmat[2, 2]
tr = m00 + m11 + m22
qw = ti.sqrt(1.0 + tr) / 2.0
qx = (m21 - m12) / (4.0 * qw)
qy = (m02 - m20) / (4.0 * qw)
qz = (m10 - m01) / (4.0 * qw)
angle = ti.acos((tr - 1.0) / 2.0)
axis = (ti.Vector([qx, qy, qz]) * (ti.sin(angle) / abs(ti.sin(angle)) + 1e-9)).normalized()
return angle * axis
@ti.kernel
def scan_aa_grid(euler_limit: ti.ext_arr()):
x_min, x_max = euler_limit[0, 0], euler_limit[0, 1]
y_min, y_max = euler_limit[1, 0], euler_limit[1, 1]
z_min, z_max = euler_limit[2, 0], euler_limit[2, 1]
for i, j, k in axis_angle:
rx = x_min + (x_max - x_min) * i / (nx - 1.0)
ry = y_min + (y_max - y_min) * j / (ny - 1.0)
rz = z_min + (z_max - z_min) * k / (nz - 1.0)
rmat = euler2rotmat(rx, ry, rz)
rvec = rotmat2rotvec(rmat)
vrgb = colormap(rvec)
axis_angle[i, j, k] = rvec
aa_colormp[i, j, k] = ti.Vector([vrgb[0], vrgb[1], vrgb[2], 0.0])
@ti.kernel
def animate_aa(t: ti.f32):
rx, ry, rz = t * 0.0011, t * 0.0012, t * 0.0015
rmat = euler2rotmat(rx, ry, rz)
for I in ti.grouped(axis_angle):
p_cam = rmat @ axis_angle[I] + ti.Vector([0.0, 0.0, t_pushed])
depth = p_cam[2]
p_img = K @ (p_cam / depth)
p_img = ti.cast(p_img, ti.i32)
aa_colormp[I][3] = depth
aa_transfm[I] = ti.Vector([p_img[0], p_img[1]])
@ti.kernel
def render():
# clear z_buffer
for I in ti.grouped(z_buff):
z_buff[I] = ti.Vector([0.0, 0.0, 0.0, t_farest])
# update z_buffer
for I in ti.grouped(aa_colormp):
depth = aa_colormp[I][3]
px, py = aa_transfm[I][0], aa_transfm[I][1]
if depth <= z_buff[px, py][3]:
z_buff[px, py] = ti.Vector([aa_colormp[I][0], aa_colormp[I][1], aa_colormp[I][2], depth])
def main():
# set euler angle limits
euler_range = np.array([
[-1.0 * PI, +1.0 * PI], # X >> [-Pi, +Pi]
[-0.1 * PI, +0.1 * PI], # Y >> [-Pi, +Pi]
[-0.6 * PI, +0.6 * PI], # Z >> [-Pi, +Pi]
], dtype=np.float64)
scan_aa_grid(euler_range)
gui = ti.GUI("LieAlgebra", res=(RES, RES))
for ts in range(1000000):
animate_aa(ts)
render()
gui.set_image(z_buff.to_numpy()[..., :3])
gui.show()
if __name__ == "__main__":
main()
顺便贴一下code, 不太会光追 只写了基本的z_buffer实现, 欢迎讨论~~
3 个赞