
在GAMES 201课程模版的基础上,完成了以下任务:
原公式:
v(t+1) = v(t) + dt * inv(M) * F(t+1)
x(t+1) = x(t) + dt * v(t+1)
修改后的公式:
v(t+1) = v(t) + dt * inv(M) * (F(t) + F(t+1)) / 2
x(t+1) = x(t) + dt * (v(t) + v(t+1)) / 2
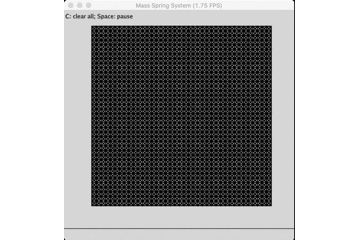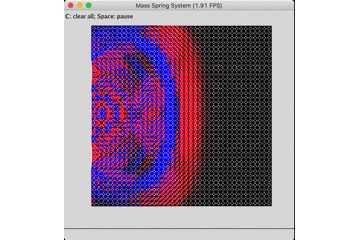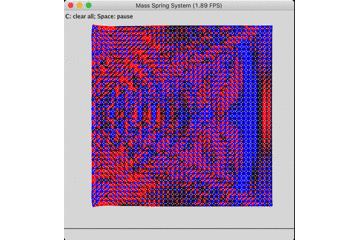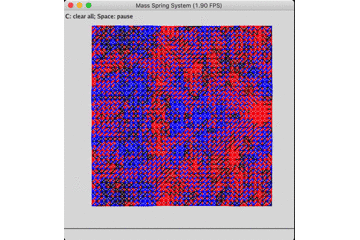
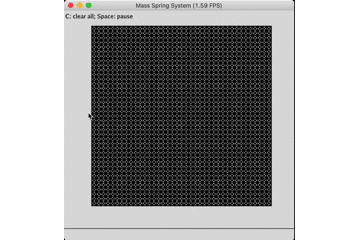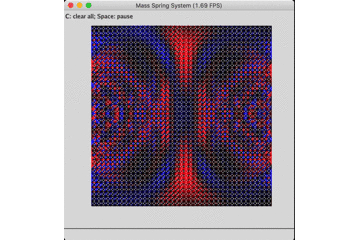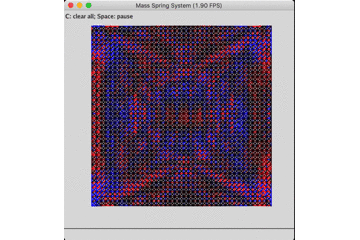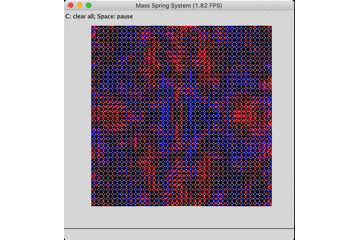
原公式的能量耗散情况如下,作为无阻尼振动仿真器的效果较差。
代码片段
@ti.func
def substep_jacobi_semi():
n = num_particles[None]
ht2 = ht * ht
# calc force
for i in range(n) :
new_force[i] = gravity * particle_mass[None]
for j in range(n) :
if rest_length[i,j] != 0 :
new_force[i] += f_ij(i,j)
# init new velocity
for i in range(n) :
new_velocity[i] = velocity[i] + new_force[i] / particle_mass[None] * dt
force[i] = new_force[i]
mass = ti.Matrix([[particle_mass[None],0.0],[0.0,particle_mass[None]]])
# fill A b
for i in range(n) :
for j in range(n) :
A[i,j] *= 0.0
for i in range(n) :
A[i,i] += mass
for j in range(n) :
if rest_length[i, j] != 0:
A[i,i] += ht2 * dfj_ij(i,j)
A[i,j] -= ht2 * dfj_ij(i,j)
for i in range(n) :
b[i] = new_force[i] * ht * 2 + mass @ velocity[i]
for j in range(n) :
if rest_length[i,j] != 0 :
b[i] -= ht2 * dfj_ij(i,j) @ velocity[i]
b[i] += ht2 * dfj_ij(i,j) @ velocity[j]
# solve equation for new velocity
solve_equation()
# Compute new position
for i in range(n) :
position[i] += (velocity[i] + new_velocity[i]) * ht
velocity[i] = new_velocity[i]
# velocity[i] *= ti.exp(-dt * damping[None]) # damping
完整代码: games201/HW2.py at master · kphmd/games201 · GitHub
没有解决的问题:
- 弹簧长度压缩到0时,弹力的方向丢失
- 弹簧长度压缩到小于0时,根据相对位置计算出弹力方向时反的,导致能量暴增。
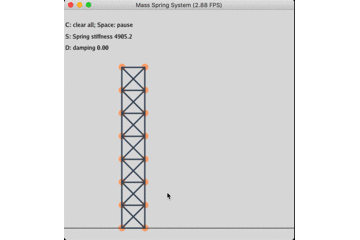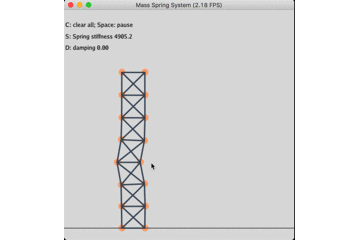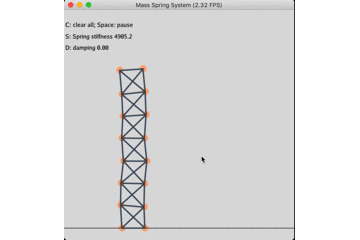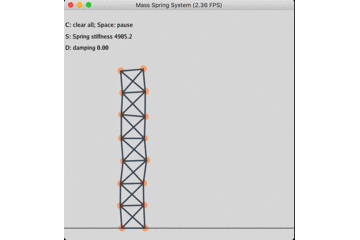
固定底座的无阻尼自由振动: