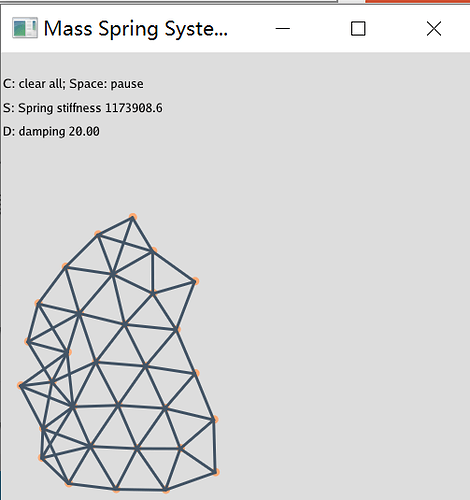
弹簧刚度超过 100 万,我们的弹簧还不爆炸。显示求解早炸了。
应该是成了
ms_implicit.py
import taichi as ti
# ti.init(debug=True, arch=ti.cpu)
ti.init(arch=ti.gpu)
## 系统参数 ===============================
MAX_NUM_PARTICLES = 256 # 最多质点数
PARTICLE_MASS = 1 # 质点质量
BOTTOM_Y = 0.05 # 地面位置
CONNECTION_RADIUS = 0.15 # 质点自动连接半径
GRAVITY = ti.Vector([0, -9.8], dt=ti.f32) # 重力场
dt = 1e-3 # 时间步长
num_particles = ti.var(ti.i32, shape=()) # 现有质点数
spring_stiffness = ti.var(ti.f32, shape=()) # 弹簧刚度
paused = ti.var(ti.i32, shape=()) # 暂停
damping = ti.var(ti.f32, shape=()) # 阻尼
# rest_length[i, j] = 0 则 i,j 未连接
rest_length = ti.var(ti.f32, shape=(MAX_NUM_PARTICLES, MAX_NUM_PARTICLES))
x = ti.Vector(2, dt=ti.f32, shape=MAX_NUM_PARTICLES) # 位置
v = ti.Vector(2, dt=ti.f32, shape=MAX_NUM_PARTICLES) # 速度
M = ti.Matrix(2, 2, dt=ti.f32, shape=(MAX_NUM_PARTICLES, MAX_NUM_PARTICLES))
J = ti.Matrix(2, 2, dt=ti.f32, shape=(MAX_NUM_PARTICLES, MAX_NUM_PARTICLES))
A = ti.Matrix(2, 2, dt=ti.f32, shape=(MAX_NUM_PARTICLES, MAX_NUM_PARTICLES))
F = ti.Vector(2, dt=ti.f32, shape=MAX_NUM_PARTICLES)
b = ti.Vector(2, dt=ti.f32, shape=MAX_NUM_PARTICLES)
spring_stiffness[None] = 10000
damping[None] = 20 # 恒定阻尼
## 速度求解器 =====================================
@ti.kernel
def symplectic_euler():
"半隐式欧拉法"
n = num_particles[None]
k = spring_stiffness[None]
m, g = PARTICLE_MASS, GRAVITY
for i in range(n):
v[i] *= ti.exp(-dt * damping[None]) # 计算阻尼
f = m * g
for j in range(n):
l_ij = rest_length[i, j]
if l_ij != 0: # 两质点间有弹簧连接
x_ij = x[i] - x[j]
f += -k * (x_ij.norm() - l_ij) * x_ij.normalized()
# `dv = dt * a = dt * (f / m)`
v[i] += dt * (f / m)
## 隐式欧拉法 --------------
@ti.kernel
def init_M():
"""初始化质量矩阵 M
"""
m = ti.Matrix([
[PARTICLE_MASS, 0],
[0, PARTICLE_MASS]
])
for i in range(num_particles[None]):
M[i, i] = m
@ti.kernel
def update_J():
"""更新 jacobi 矩阵
- [Miles Macklin](https://blog.mmacklin.com/2012/05/04/implicitsprings/)
"""
I = ti.Matrix([
[1.0, 0.0],
[0.0, 1.0]
])
k = spring_stiffness[None]
for i, d in J: # 遍历 J
# i 为观察的质点
# d 为求导数的方向 x_d
for j in range(num_particles[None]): # 遍历所有点
l_ij = rest_length[i, j] # 对于弹簧 i <-- j
if (l_ij != 0) and (d == i or d == j):
# i,j 间有弹簧链接 && 求导方向 d 为 i 或 j
x_ij = x[i] - x[j]
X_ij_bar = x_ij / x_ij.norm()
mat = X_ij_bar.outer_product(X_ij_bar)
J[i, d] += -k * (I - l_ij/x_ij.norm() * (I - mat))
if d==i:
J[i, d] *= 1.0
else: # d==j
J[i, d] *= -1.0
@ti.kernel
def update_A(beta: ti.f32):
"""更新 A
A = M - dt^2 * J(t)
"""
# beta = 0.5
for i, j in A:
A[i, j] = M[i, j] - beta * dt**2 * J[i, j]
@ti.kernel
def update_F():
"""计算 x 的受到的合力
"""
k = spring_stiffness[None]
m, g = PARTICLE_MASS, GRAVITY
for i in range(num_particles[None]):
F[i] = m * g
for i, j in rest_length:
l_ij = rest_length[i, j]
if l_ij != 0:
x_ij = x[i] - x[j]
F[i] += -k * (x_ij.norm() - l_ij) * x_ij.normalized()
else: # l_ij == 0
pass # i,j 间无弹簧
@ti.kernel
def update_b():
"""更新 b
b = M*v_star + dt * F(t)
v_star = v(t) + dt * a(t)
`a(t)` 其他力导致的加速度。如:damping、相对速度
"""
for i in range(num_particles[None]):
v_star = v[i] * ti.exp(-dt * damping[None])
b[i] = A[i, i] @ v_star + dt * F[i]
@ti.kernel
def jacobi():
"""Jacobi 迭代
A = M - dt^2 * J(t)
b = M * v(t) + dt * F(t)
A * v(t+1) = b
"""
n = num_particles[None]
for i in range(n):
for j in range(n):
if i != j:
b[i] -= A[i, j] @ v[j]
v[i] = A[i, i].inverse() @ b[i]
def implicit_euler(beta=0.5):
"""隐式欧拉法 + Jacobi 迭代
A = M - beta * dt^2 * J(t)
b = M*v(t) + dt * F(t)
A * v(t+1) = b
### beta
= 0.0: forward/semi-implicit Euler (explicit)
= 0.5: middle-point (implicit)
= 1.0: backward Euler (implicit)
### step
0. 初始化 M
1. 更新 J(t)
2. 更新 A
3. 更新 F(t)
4. 更新 b
5. 求解 v(t+1)
"""
init_M()
update_J()
update_A(beta)
update_F()
update_b()
jacobi()
## 通用步骤 ====================================
@ti.kernel
def collide():
"""与地面碰撞"""
for i in range(num_particles[None]):
if x[i][1] < BOTTOM_Y:
x[i][1] = BOTTOM_Y
v[i][1] = 0
@ti.kernel
def update_position():
"""更新位置
x(t+1) = x(t) + dt * v(t+1)
"""
for i in range(num_particles[None]):
x[i] += v[i] * dt
def substep():
"一个时间步长"
# symplectic_euler() # 半隐式欧拉法
implicit_euler(1.0) # 隐式欧拉法/后向欧拉法
collide()
update_position()
@ti.kernel
def add_particle(pos_x: ti.f32, pos_y: ti.f32):
"添加新质点"
new_particle_id = num_particles[None]
x[new_particle_id] = [pos_x, pos_y]
v[new_particle_id] = [0, 0]
num_particles[None] += 1
# Connect with existing particles
for i in range(new_particle_id):
dist = (x[new_particle_id] - x[i]).norm()
if dist < CONNECTION_RADIUS: # 与指定半径内的点建立连接
rest_length[i, new_particle_id] = 0.1
rest_length[new_particle_id, i] = 0.1
## GUI =====================================
gui = ti.GUI('Mass Spring System', res=(512, 512), background_color=0xdddddd)
add_particle(0.3, 0.3)
add_particle(0.3, 0.4)
add_particle(0.4, 0.4)
while True:
for e in gui.get_events(ti.GUI.PRESS):
if e.key in [ti.GUI.ESCAPE]:
exit()
elif e.key == gui.SPACE:
paused[None] = not paused[None]
elif e.key == ti.GUI.LMB:
add_particle(e.pos[0], e.pos[1])
elif e.key == 'c':
num_particles[None] = 0
rest_length.fill(0)
elif e.key == 's':
if gui.is_pressed('Shift'):
spring_stiffness[None] /= 1.1
else:
spring_stiffness[None] *= 1.1
elif e.key == 'd':
if gui.is_pressed('Shift'):
damping[None] /= 1.1
else:
damping[None] *= 1.1
if not paused[None]:
for _ in range(10): # 10 小步为一帧
substep()
## 绘制
# 地板
gui.line(begin=(0.0, BOTTOM_Y), end=(1.0, BOTTOM_Y), color=0x0, radius=1)
# ms 系统
X = x.to_numpy()
gui.circles(X[:num_particles[None]], color=0xffaa77, radius=5)
for i in range(num_particles[None]):
for j in range(i + 1, num_particles[None]):
if rest_length[i, j] != 0:
gui.line(begin=X[i], end=X[j], radius=2, color=0x445566)
## 显示系统参数
gui.text(content=f'C: clear all; Space: pause', pos=(0, 0.95), color=0x0)
gui.text(content=f'S: Spring stiffness {spring_stiffness[None]:.1f}', pos=(0, 0.9), color=0x0)
gui.text(content=f'D: damping {damping[None]:.2f}', pos=(0, 0.85), color=0x0)
gui.show()
Jacobi 矩阵
根据 Miles Macklin 给出的公式稍微化简了下
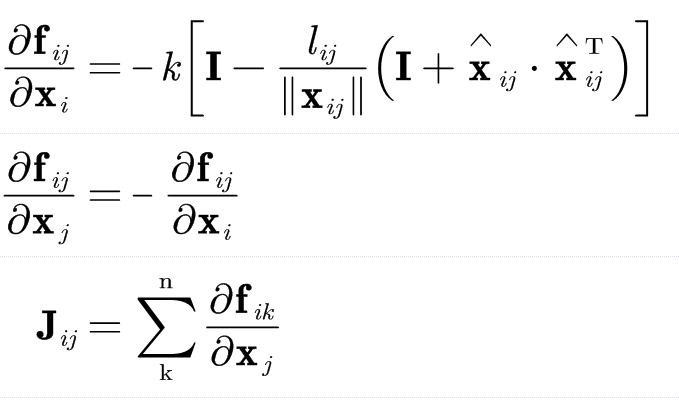
equ LaTeX
$$
\frac{\partial \mathbf{f}_{ij}}{\partial \mathbf{x}_i}=-k\left[ \mathbf{I}-\frac{l_{ij}}{\lVert \mathbf{x}_{ij} \rVert}\left( \mathbf{I}+\widehat{\mathbf{x}}_{ij}\cdot \widehat{\mathbf{x}}_{ij}^{\text{T}} \right) \right]
\\
\frac{\partial \mathbf{f}_{ij}}{\partial \mathbf{x}_j}=-\frac{\partial \mathbf{f}_{ij}}{\partial \mathbf{x}_i}
\\
\mathbf{J}_{ij}=\sum_{\text{k}}^{\text{n}}{\frac{\partial \mathbf{f}_{ik}}{\partial \mathbf{x}_j}}
$$
跑起来感觉没问题
(看上去是写对了,jacobi 矩阵的推导先咕咕咕
我听说有个方法叫 Jacobian-free Newton Krylov,那可太棒了。坐等 lec 04
求导是不可能求的,只能看别人的结果推一推过程这样。