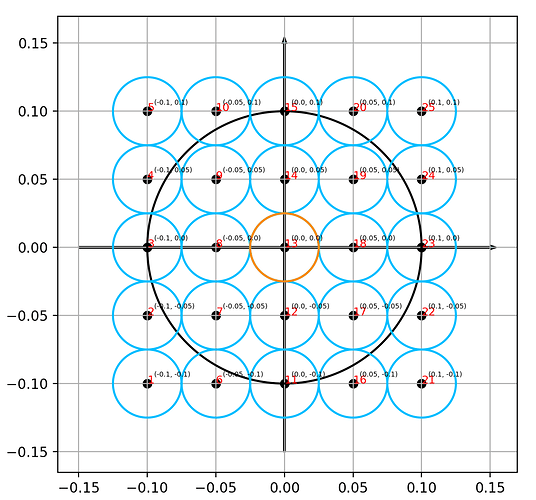
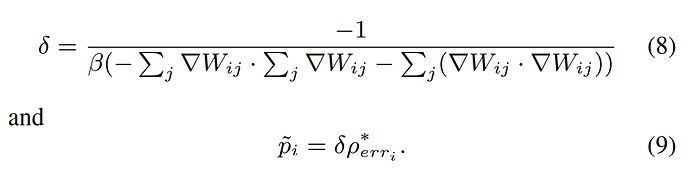请教关于PCISPH中的系数

综合讨论区
#1

各位老师好，

熟悉SPH的同学你们好

请问PCISPH中的那个系数delta，如下

image
image1291×329 22.3 KB

为什么能是一个常数呢？

它对i的邻域粒子j进行求和，难道不是只针对粒子i有效吗？那不应该是每个粒子i都有独自的一个delta吗？

还是说随意取一个粒子i使用上述公式？

公式参考自
B. Solenthaler and R. Pajarola. 2009. Predictive-corrective incompressible SPH. ACM Trans. Graph. 28, 3, Article 40 (August 2009), 6 pages. DOI:https://doi.org/10.1145/1531326.1531346

1 个赞
#2

由于如果对于每个粒子都去计算系数，在一些情况下，比如自由液面附近的粒子会有particle deficiency的问题，导致算出来的值偏差较大，因此这里可以认为是用一个perfect sampling的情况去近似一个比较好的系数，可以用于所有粒子

perfect sampling:

image
image442×604 16.8 KB

图源: Dan Koschier, Jan Bender, Barbara Solenthaler, Matthias Teschner, “Smoothed Particle Hydrodynamics for Physically-Based Simulation of Fluids and Solids”, Eurographics Tutorial, 2019

3 个赞
#3

参照SPLISHSPLASH那个库，又学习了一下它的代码，于是发现所谓perfect sampling是这样的：

PCI
PCI1087×1013 137 KB

(画出来结果和mzhang 助教 所说一致)

蓝色小圈代表邻居粒子
橙色小圈是当前粒子
黑色大圈是核半径

这里取粒子半径为0.025
核半径是粒子半径的四倍

只要比较各个蓝色小圆的中心点是不是在黑色大圈里面就行了

于是这就是perfect sampling(SplishSPlasH的）

画图的代码如下

import numpy as np
import math
import matplotlib.pyplot as plt

def circle(x,y,r,color='k',count=1000):
    xarr=[]
    yarr=[]
    for i in range(count):
        j = float(i)/count * 2 * np.pi
        xarr.append(x+r*np.cos(j))
        yarr.append(y+r*np.sin(j))
    plt.plot(xarr,yarr,c=color)

hp = 0.025
h = 4* hp
diam =2*hp
xi = [0, 0]
xj =[-h,-h]

print("h=",h,"diam=",diam)
i,j=0,0

fig1 = plt.figure(num='fig1',figsize=(6,6),dpi=100,facecolor='#FFFFFF',edgecolor='#FF0000')
plt.grid()


plt.arrow(-0.15,0,0.3,0)
plt.arrow(0,-0.15,0,0.3)

circle(0,0,h)

while(xj[0]<=h):
    print("")
    print("") 
    print("loop0 ")   
    while(xj[1]<=h):
        j=j+1
        print("loop1")
        print("xi=",xi,"xj=",xj)
        
        dist2=(xi[0]-xj[0])**2 + (xi[1]-xj[1])**2
        print("dist=",math.sqrt(dist2))
        
        #画蓝色圈
        circle(xj[0],xj[1],hp,'#00BFFF')
        plt.scatter(xj[0],xj[1],c='k')
        plt.text(xj[0],xj[1],color='r',s=f'{j}',size=8)
        plt.text(xj[0]+0.005,xj[1]+0.005,color='k',s=f'{xj[0],xj[1]}',size=5)
        
        if  dist2<= h**2:
            print("yes")
        xj[1] += diam
    xj[0] += diam
    xj[1] = -h
print("end")

#画橙色圈
circle(0,0,hp,'#FF8C00')
plt.show()
3 个赞
#4

还有一个要提醒的地方，不要计算和中心粒子重合的粒子哦
因为在那里距离就是0
计算gradW的时候，由于是个向量，0向量应该是0，是任意方向的。

所以，要么定义好一个向量的gradW，当输入值为0的时候给0
或者干脆邻域不要计算0距离，直接给0

3 个赞