Tiger
2021 年11 月 13 日 08:20
#1
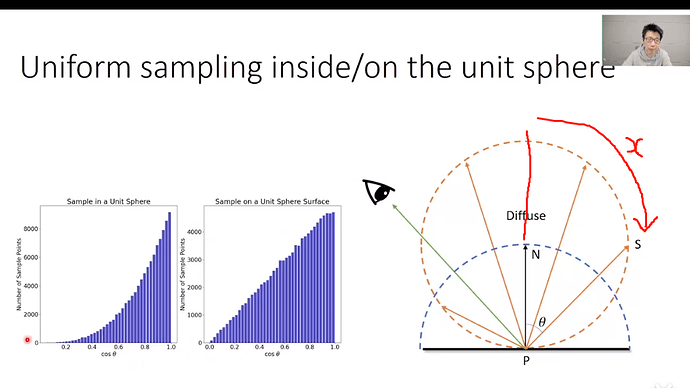
在太极图形课S1第07讲P3中16:00位置,讲到在圆面上均匀采样再转换,可以得到下图中右侧的分布 (和cos(theta)成正比)。
我对这一结果感到有些奇怪:假设从theta对应的弧长设为x(标注的红线),那么 x = r * 2 * theta,因此我似乎应当认为所述采样方式的结果应该是 theta 的某种更线性的函数关系(似乎是 theta 上均匀分布,但至少不是 cos(theta) 相关的)。
另一方面,如果考虑是三维球面,由于变换是 r^2 * sin(theta),似乎线性相关的形式也是以 sin(theta) 为变量, 而不是 cos(theta)。
不知我的想法是哪里出现了问题?
谢谢!
1 个赞
Vineyo
2021 年11 月 15 日 08:03
#2
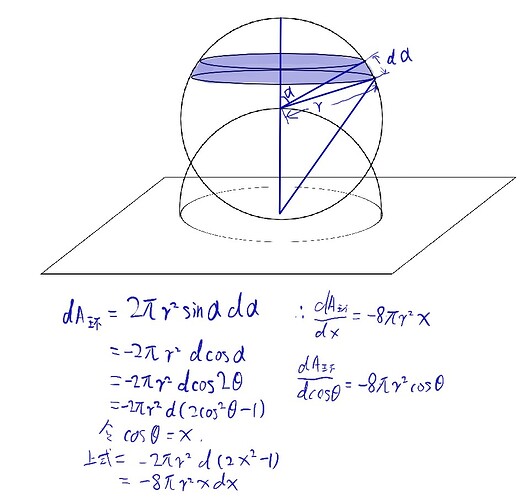
刚好我也对这个公式感兴趣,就推了一下:
然后我们求α所对的微小圆环面积:
其中dcosθ是负的,所以单位cosθ所对的面积与cosθ成正比(把cosθ换成x更容易看出)。
5 个赞
Tiger
2021 年11 月 15 日 10:53
#3
谢谢你的帮助,这个推导是正确的,根据这一推导我理解了之前统计结果呈现直线这一结论!
不过,我有一点还是略微困惑:
这里的结果,相当于(公式忽略常数)使得概率密度函数为 p(cos(\theta))= cos(\theta) 。另一方面,我理解这里应该是需要使得 p(\theta)= cos(\theta) ,来满足例如 Lambertian 反射模型的需要。
这两者似乎相互冲突,不知我的理解问题出在哪里?
谢谢!
Vineyo
2021 年11 月 15 日 11:50
#4
你可以写成 p=cos(θ) ,是 p(θ) 还是 p(x) 只是符号上不同。我倒没注意到这个跟 Lambertian 反射模型的关系,感觉课上可以补充一下。
1 个赞
Tiger
2021 年11 月 15 日 13:23
#5
嗯嗯,Lambertian 反射模型就是按角度等概率采样,然后乘上 cos(\theta) 作为强度。如果没有理解错的话,这里就是把强度换成概率。你推导里的变量代换是没问题的,只是这结果我个人感觉不是和原模型一致的(不过因为课上说这是书上的公式,大概率是我哪里想错了……)。
如果有老师看到这里,后面课上也再请老师补充补充!
谢谢!
Tiger
2021 年11 月 18 日 12:18
#6
因答疑课上语音或许不好表达清楚,这里补充一下推导过程(附图可参考上面Vineyo推导),请老师指正!
Hi Tiger,
你的推导完全没有问题:)但是你的假设有问题。
事实上,需要在半球面上做到均匀采样,关于theta的概率密度应该为为p(theta) = sin(theta),这个在课件上也有简易的推导。所以在球面上对cos(theta)做重要性采样时,关于theta的概率密度应该为p(theta)=sin(theta)cos(theta)=1/2sin(2 theta),这也和你之后的推导吻合。
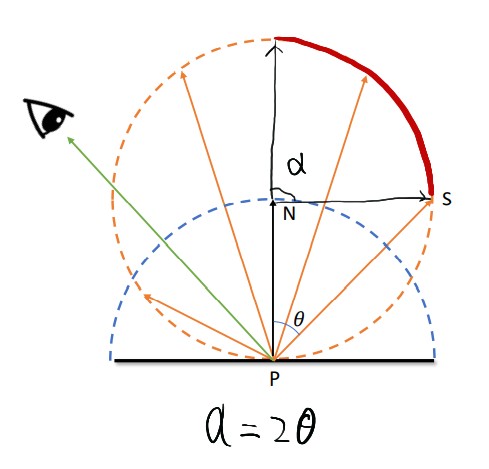
这也是为什么我们可以在角度为2theta球面上采样再投影回半球面的直观理由。抱歉这一段因为时间问题在课上没有仔细推导。
Best,
7 个赞
Tiger
2021 年11 月 20 日 01:50
#8
原来我之前是弄错了假设,现在明白了!谢谢天添老师!
1 个赞