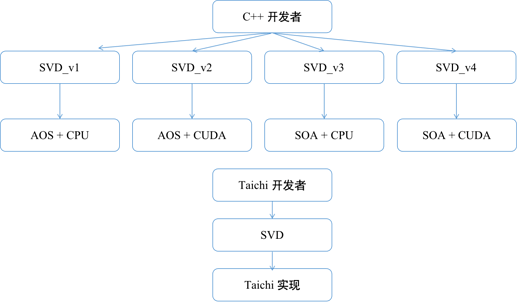
Taichi 语言中提供了很多好用的小矩阵库函数，方便大家在 Taichi kernel 中调用。这篇文章中将会给大家展示这些函数如何提高生产力而不降低性能。
同时这也是一篇呼吁大家提 Feature Request 的文章。期待大家提供更多你想要的小矩阵相关功能。欢迎在 GitHub Discussion 讨论贴中留言提“需求”，也欢迎感兴趣的社区同学和我们一起开发！
有好奇心的各位朋友在自己的学习和工作生涯里，可能都或多或少的做过重复造轮子的事情，造轮子这件事的利弊不能一概而论。在学习某些技术的过程中，造轮子可能会帮助我们更深入的了解技术细节，提升我们的个人能力。当然也会有大佬青出于蓝，造出更厉害的轮子出来，从小木轮造成了跑车轮子。但在生产环境中，重复造轮子可能并不是个明智的选择。很多时候，我们自己写出来的代码并不能超越一些已有的开源库，因为这些库的实现需要深厚的背景知识和实践积累。
比如在工程领域，涉及很多数值计算相关的算法。 数值计算中最关键的往往就是对矩阵、向量的操作以及线性系统 Ax = b 的求解。
现实中，这样的线性系统往往还很大，有可能上百万个未知数。为了求解这些线性系统，科学家们开发了很多线性代数相关的数学库。比如：Intel 基于自家 CPU，充分利用其多核多线程并行能力推出的数学库：Intel(R) oneAPI Math Kernel Library；NVIDIA 基于自家 GPU 并行能力推出的 CUDA Toolkits，其中提供了 cuBLAS， cuSparse，cuSolver 等数学库。
很多时候，我们可以直接调用这些库来实现一些线性系统的求解，而不用担心这些库怎么实现多核/多线程并行的。这些库的开发者一般都有深厚的数学背景和工程能力，能够很好的基于硬件进行极致的优化。这时候我们要是再自己重复造轮子，恐怕只会费力不讨好。
那什么时候需要用户自己造轮子呢？一种情况是适配的库不好找。拿一个物理仿真的例子来说，在 FEM 弹性物体仿真中我们常常会使用 SVD 分解来判断计算单元是否翻转 ¹。在 CPU 中，比较方便的办法是直接调用类似于 Eigen 这样的数学库。而在 GPU 中，可以在并行的核函数内被调用的 SVD 分解库就很难找了。
另一种情况是现有库的实现为了保证通用性而难以在所有的使用环境下都保证性能最优，所以在特定的环境下，用户会愿意手写更高效的实现。还是拿刚才的 SVD 分解举例，在限定了矩阵大小是 3 \times 3 的特定环境下，量身定制的方式可以极大加速这样的矩阵分解。所以 A. McAdams, E. Sifakisd, J. Teran 等人就专门针对 3 \times 3 矩阵写了一个基于 CPU 的 SVD 分解程序²。该算法能够把 3 \times 3 SVD 分解从Computation Bound 变成 Memory Bound，极大的加速了计算效率。这也是 Taichi 中 3 \times 3 矩阵 SVD 分解的实现 ³。
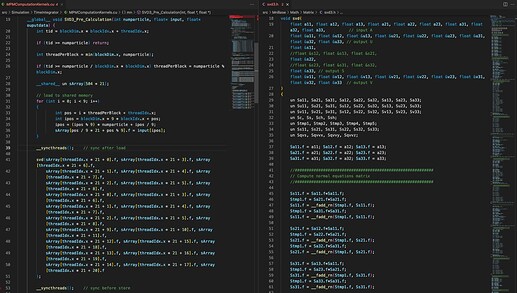
在 GPU 的 CUDA kernel 中想要局部的调用 3 \times 3 矩阵的 SVD 分解函数，就只能老老实实自己手写了。但实现起来就更加麻烦了，写起来也很让人痛苦，还不一定正确。为此 Kui Wu 等人又针对 GPU 写了一个 CUDA 版本的 3 \times 3 矩阵的 SVD 分解，我们可以调用他们的实现 ⁴。但这样做同样有很多缺点：
- 需要根据不同的数据结构（SOA/AOS）来调用不同的 SVD 分解函数 ⁵。
#ifdef USE_SOA
svd3_SOA << <pblks, threads >> >(d_input, d_answer, n);
#else
svd3_AOS_shared << <pblks, threads >> >(d_input, d_answer, n);
#endif // USE_SOA
- 使用的时候代码冗长。
然而在 Taichi 里面，不管是使用 CPU 还是 GPU 作为计算硬件，调用一个 3 \times 3 矩阵的 SVD 分解只需要简单的如下几行代码：
@ti.kernel
def test_svd():
A = ti.Matrix([[1,2,3],[4,5,6],[7,8,9]])
U, S, V = ti.svd(A)
Taichi统一函数接口，简化了用户的代码，提高了生产力
像 SVD 分解这种很高频的基础函数，如果每次自己手动去实现，还要考虑不同后端和不同数据结构产生的差异，那么很可能会出现各种 bug，也会降低工作效率。而 Taichi 已经提供了小矩阵（ 2 \times 2 和 3 \times 3 ）相关的一些基础的操作，比如 SVD 分解，QR 分解，线性方程组求解，特征值分解等 常用的功能，而且你也不用担心不同后端，不同数据结构的不同实现问题。
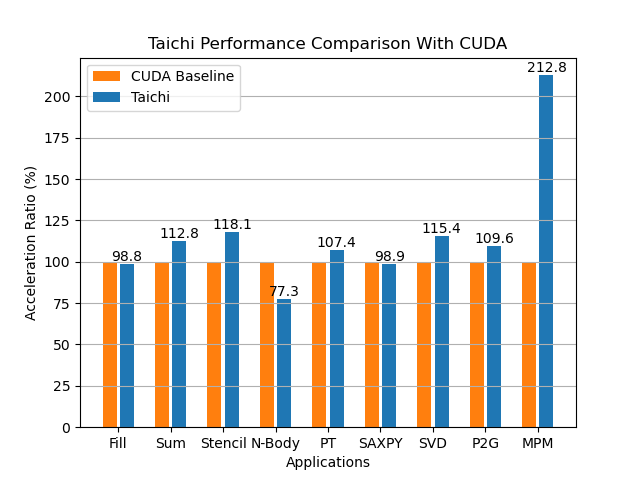
Taichi 在不同算法上相对 CUDA 的加速比，单位是百分比，计算方法为 CUDA 运行时间/Taichi 运行时间。在每项测试中我们都会测试多种不同的算法参数，图中统计的加速比是全部结果的平均值。
除此之外，你可能也会担心性能问题。在这篇文章中
与 CUDA 相比，Taichi 跑得快不快？我们基于多个算例（比如 SVD，SAXPY）对比了 Taichi 和 CUDA 的性能。从对比中，我们可以看到 Taichi 在并行优化上能够充分发挥设备的计算性能。
我们相信， 3 \times 3 矩阵的 SVD 分解只是一大堆小规模，kernel 内调用线性代数操作中的沧海一粟，平时大家自己一定还有不少写出老茧来的小规模函数。
欢迎大家把你在工程实现中常用到的一些小矩阵相关的操作，或者那些经常让你写到手软的 CUDA kernel 函数，在 Github Discussion 中（点击 GitHub Discussion 讨论贴即可访问）留言，也可以加入 Slack 的 Taichi 语言社区交流频道畅所欲言。
期待大家多多提 Feature Request，我们将逐步完善相关的功能，提供更多的工具，减少造轮子的烦恼，解放更多生产力！
部分图片来源于网络如有侵权请联系我们
References:
1.https://www.math.ucla.edu/~jteran/papers/ITF04.pdf
2.Research projects of Eftychios Sifakis
3.taichi/sifakis_svd.h at master · taichi-dev/taichi · GitHub
4.GitHub - kuiwuchn/3x3_SVD_CUDA: Fast CUDA 3x3 SVD
5.3x3_SVD_CUDA/kernel.cu at 74ac0dc12fe8bbe2f3be9d154af8515f66ae5786 · kuiwuchn/3x3_SVD_CUDA · GitHub
Slack 频道：
https://join.slack.com/t/taichicommunity/shared_invite/zt-14ic8j6no-Fd~wKNpfskXLfqDr58Tddg