Hi guys, I am having a bit of trouble with descibing a polygon in a 2d grid, hoping someone could suggest anything. Thx in advance
I couldn’t find a proper way to handle geometry of an cell using immerased boundary method in a fixed grid i.e. 1000 x 1000. My overall goal is to re-implemente the LBIBCell in Taichi. However, it seems pretty difficult to for me to think of a way for the shape of a polygon (cell) in lattice grid in Taichi.
I have the code here: https://github.com/wyq977/taichi_lbibcell
As shown in the gif on homepage, the simulation went well for Computational fluid dynamics (CFD) using Lattice Boltzmann methods, inspired by LBM_Taichi.
Since I cannot init. another variable to store upon each iteration, one has to come up with a plan to store a list of points (f32 or f64) and their connection.
Also, because the polygon (cell) are subject to tension/forces between each other, increasing mass (not described here) one has to find a way to remesh the polygon and finally divide along the longest axis or a random axis (representing cell division).
To put it simply, one has to come up with the following functionality to describe the reaction-diffusion as well as the fluid dynamics:
- Find the cloestest lattice grid
point(i, j)to the polygon geometry, (kind of done, see below, i, j are integer - Mark the cloestest as inner or outer
- Remesh the geometry:
- For example, the 4 points for the cubes are too far away from each other, more points have to be inserted between those 4 points to capture the forces (tension)
- Divide a polygon along certain axis
In the final version or current LBIBCell, the number of cells are not fixed due to division.
self.boundary = ti.Vector.field(2, dtype=ti.f32, shape=(4,)) # store 4 points of a cube
Currently, I could have one or mulutple variables representing multiple polygon (cell) geometry in the beginning. But the problem with that, I limit the resolution of the polygon since I cannot change/remesh edges/connecion later in simulation.
Ideal situation would be like this:
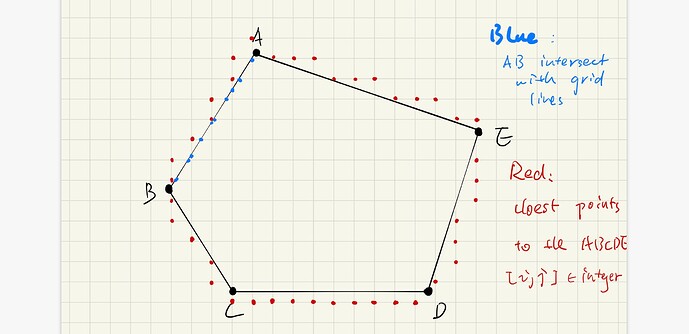
LBIBCell’s way to finding cloest grid points, figure of illustration below
- for each edge (connection) AB, calculate all the coordiantes of points that AB intersects with grid line (x=1, 2,… and y = 1,2,…),basically finds the y=ax +b from AB cooridnates
- Finds the closts grid point
p(i, j)to those intersection - Find out the ones that are outside of the polygon
Since polygon like ABCDE may have edges horizontally or vertically align with the gird/axis, a little pertubation will be done before to avoid cases like AB is parallel to x = 0 or y = 0.
Thx you guys in advance and any suggestions would be much appreciated