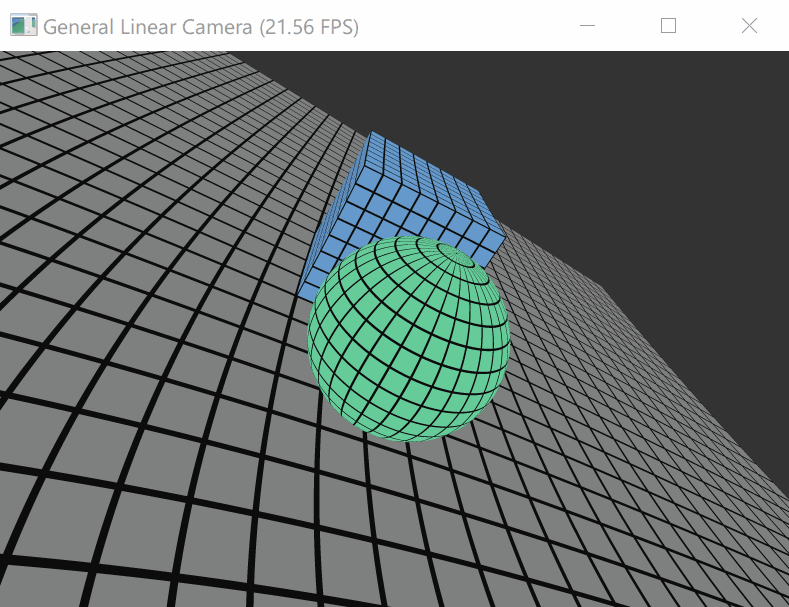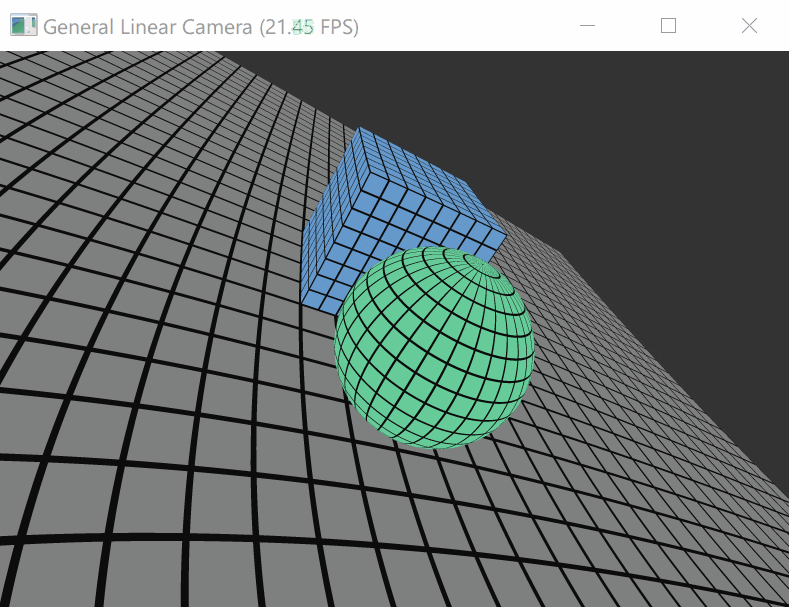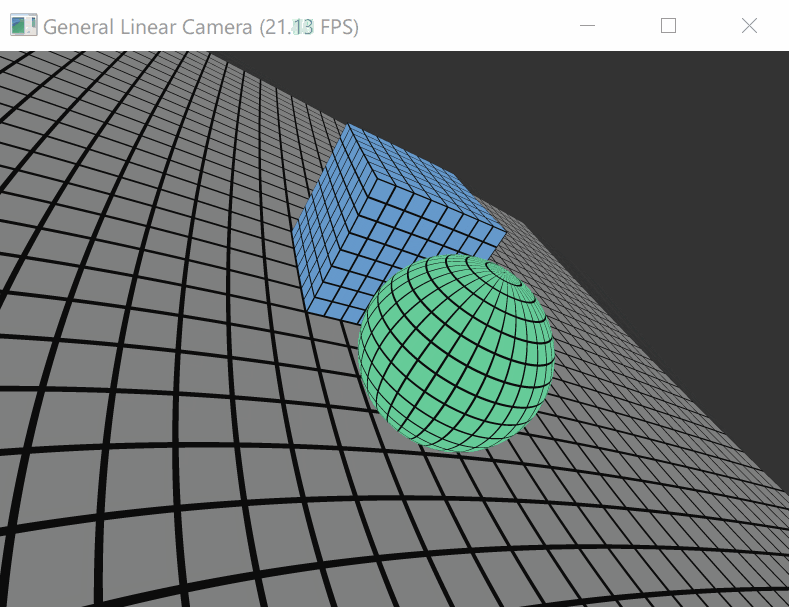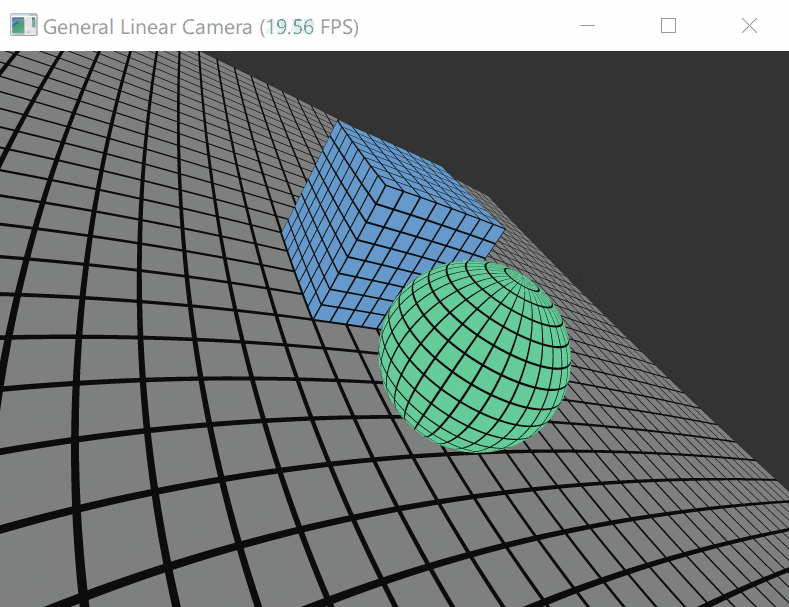
不会流体力学,那模拟个非传统的相机好了,就当taichi上手练习:
Yu, Jingyi, and Leonard McMillan. “General linear cameras.” European Conference on Computer Vision . Springer, Berlin, Heidelberg, 2004.
#/usr/bin/python
import taichi as ti
import math
ti.init(arch=ti.gpu)
kWidth = 800
kHeight = 600
pixels = ti.Vector(3, dt=ti.f32, shape = (kWidth, kHeight))
@ti.func
def mesh_texture(uv, uscale, vscale, bright_color) -> ti.Vector:
s = uv[0] * uscale
t = uv[1] * vscale
s = s - ti.cast(s, ti.i32)
t = t - ti.cast(t, ti.i32)
color = bright_color
if s < 0.05 or t < 0.05 or s > 1-0.05 or t > 1-0.05:
color = ti.Vector([0.05, 0.05, 0.05])
return color
@ti.func
def sphere_pos_to_uv(local_pos) -> ti.Vector:
p = local_pos.normalized()
# p.y = cos(theta)
theta = ti.acos(p[1])
phi = ti.atan2(p[2], p[0])
if phi < 0:
phi += math.pi
return ti.Vector([phi / (2*math.pi), theta / math.pi])
@ti.func
def intersect_sphere(ray_o, ray_dir):
isect_pos = ti.Vector([0.0, 0.0, 1000000000.0])
isect_normal = ti.Vector([0.0, 0.0, 0.0])
isect_uv = ti.Vector([-1.0, -1.0])
# Intersects the ray with a sphere.
# ---------------------------------
# (ro + t*rd - sphere_center)^2 = radius^2
# (t*rd)^2 + (ro - sc)^2 + 2*(t*rd)*(ro-sc) = radius^2
kSphereCenter = ti.Vector([2.0, 1.0, 0.0])
kRadius = 1.0
a = ray_dir.dot(ray_dir)
b = 2*ray_dir.dot(ray_o - kSphereCenter)
c = (ray_o - kSphereCenter).dot(ray_o - kSphereCenter) - kRadius**2
# Solves the quadratic a * t^2 + b * t + c = 0
delta = b*b - 4*a*c
t_candidate = math.inf
if delta < 0:
pass
else:
t0 = (-b + ti.sqrt(delta)) / (2*a)
t1 = (-b - ti.sqrt(delta)) / (2*a)
# `a` is positive so t0 is larger than t1.
if (t1 > t0):
t1, t0 = t0, t1
t_candidate = t1
if t_candidate < 0:
t_candidate = t0
if t_candidate > 0:
isect_pos = ray_o + t_candidate * ray_dir
isect_normal = (isect_pos - kSphereCenter).normalized()
isect_uv = sphere_pos_to_uv(isect_pos - kSphereCenter)
else:
# If both t0 and t1 are negative, then the ray doesn't hit the sphere.
# ray_t value can be considered math.inf then.
t_candidate = math.inf
return isect_pos, isect_normal, isect_uv, t_candidate
# Computes intersection with floor (plane y = 0).
@ti.func
def intersect_floor(ray_o, ray_dir):
floor_normal = ti.Vector([0.0, 1.0, 0.0])
# Solves the formula: ray_o.y + t*ray_dir.y = 0
isect_pos = ti.Vector([0.0, 0.0, 0.0])
isect_normal = ti.Vector([0.0, 0.0, 0.0])
isect_uv = ti.Vector([-1.0, -1.0])
t = -ray_o[1] / ray_dir[1]
if t < 0:
# Floor is behind the ray.
t = math.inf
else:
isect_pos = ray_o + t*ray_dir
isect_normal = floor_normal
isect_uv = ti.Vector([isect_pos[0], isect_pos[2]])
isect_uv -= ti.floor(isect_uv)
# The floor is finite-sized.
if ti.abs(isect_pos[0]) > 10 or ti.abs(isect_pos[2]) > 10:
t = math.inf
return (isect_pos, isect_normal, isect_uv, t)
# Computes intersection with an AABB cube.
@ti.func
def intersect_cube(ray_o, ray_dir):
# x: [-1.5, 0.5], y: [0, 2], z: [-1, 1]
xmin, xmax = -1.5, 0.5
ymin, ymax = 0.0, 2.0
zmin, zmax = -1, 1
# Solves: ro + t*rd == [x|y|z][min|max]
t_side_a = (ti.Vector([xmin, ymin, zmin]) - ray_o) / ray_dir
t_side_b = (ti.Vector([xmax, ymax, zmax]) - ray_o) / ray_dir
txmin = ti.min(t_side_a[0], t_side_b[0])
tymin = ti.min(t_side_a[1], t_side_b[1])
tzmin = ti.min(t_side_a[2], t_side_b[2])
txmax = ti.max(t_side_a[0], t_side_b[0])
tymax = ti.max(t_side_a[1], t_side_b[1])
tzmax = ti.max(t_side_a[2], t_side_b[2])
tmin_argmax = 2
if txmin > tzmin:
tmin_argmax = 0
if tymin > txmin and tymin > tzmin:
tmin_argmax = 1
isect_pos, isect_normal, isect_uv = ti.Vector([0.0, 0.0, 0.0]), ti.Vector([0.0, 0.0, 0.0]), \
ti.Vector([-1.0, -1.0])
t = math.inf
t_earliest_exit = ti.min(txmax, ti.min(tymax, tzmax))
t_latest_enter = ti.max(txmin, ti.max(tymin, tzmin))
if t_earliest_exit < t_latest_enter:
pass
elif tmin_argmax == 0:
t = txmin
isect_pos = ray_o + t * ray_dir
isect_normal = ti.Vector([-ray_dir[0], 0.0, 0.0])
isect_uv = ti.Vector([isect_pos[1], isect_pos[2]])
elif tmin_argmax == 1:
t = tymin
isect_pos = ray_o + t * ray_dir
isect_normal = ti.Vector([0.0, -ray_dir[1], 0.0])
isect_uv = ti.Vector([isect_pos[2], isect_pos[0]])
else:
t = tzmin
isect_pos = ray_o + t * ray_dir
isect_normal = ti.Vector([0.0, 0.0, -ray_dir[2]])
isect_uv = ti.Vector([isect_pos[0], isect_pos[1]])
isect_uv = isect_uv - ti.floor(isect_uv)
return (isect_pos, isect_normal, isect_uv, t)
# Computes the closest intersection from the ray to the scene.
# The scene data is hard-coded inside this function.
@ti.func
def compute_radiance(ray_o, ray_dir):
isect_pos = ti.Vector([0.0, 0.0, 1000000000.0])
isect_normal = ti.Vector([0.0, 0.0, 0.0])
isect_uv = ti.Vector([-1.0, -1.0])
ray_t = math.inf
radiance = ti.Vector([0.0, 0.0, 0.0])
sphere_pos, sphere_normal, sphere_uv, sphere_t = intersect_sphere(ray_o, ray_dir)
if sphere_t < ray_t:
ray_t = sphere_t - 1e-6
isect_pos, isect_normal, isect_uv = sphere_pos, sphere_normal, sphere_uv
radiance = mesh_texture(isect_uv, 32, 16, ti.Vector([0.4, 0.8, 0.6]))
cube_pos, cube_normal, cube_uv, cube_t = intersect_cube(ray_o, ray_dir)
if cube_t < ray_t:
ray_t = cube_t - 1e-6
isect_pos, isect_normal, isect_uv = cube_pos, cube_normal, cube_uv
radiance = mesh_texture(isect_uv, 4, 4, ti.Vector([0.4, 0.6, 0.8]))
plane_pos, plane_normal, plane_uv, plane_t = intersect_floor(ray_o, ray_dir)
if plane_t < ray_t:
ray_t = plane_t - 1e-6
isect_pos, isect_normal, isect_uv = plane_pos, plane_normal, plane_uv
radiance = mesh_texture(isect_uv, 2, 2, ti.Vector([0.5, 0.5, 0.5]))
return ray_t < math.inf, radiance
@ti.func
def compute_barycentric_coord(a: ti.Vector, b: ti.Vector, c: ti.Vector, p: ti.Vector) -> ti.Vector:
# S_abp = ab x ap / 2
# S_abc = ab x ac / 2
(pa, pb, pc) = a-p, b-p, c-p
(ca, cb) = a-c, b-c
S_abp = pa[0] * pb[1] - pa[1] * pb[0]
S_bcp = pb[0] * pc[1] - pb[1] * pc[0]
S_cap = pc[0] * pa[1] - pc[1] * pa[0]
S_abc = ca[0] * cb[1] - ca[1] * cb[0]
return ti.Vector([S_bcp / S_abc, S_cap / S_abc, S_abp / S_abc])
@ti.kernel
def paint(frame_count: ti.f32):
distance = frame_count / 400 + 1
camera_c = ti.Vector([0.0, 0.0, distance])
# Defines the GLC.
GLC_rotate_angle = 0.3 # Change angle to 0 for a standard pinhole camera.
cos_angle, sin_angle = ti.cos(GLC_rotate_angle), ti.sin(GLC_rotate_angle)
GLC_rotater = ti.Matrix([[cos_angle, -sin_angle], [sin_angle, cos_angle]])
A1 = GLC_rotater @ ti.Vector([0.0, 0.7])
B1 = GLC_rotater @ ti.Vector([-0.7, -0.7])
C1 = GLC_rotater @ ti.Vector([0.7, -0.7])
A0 = ti.Vector([0.0, 0.4])
B0 = ti.Vector([-0.4, -0.4])
C0 = ti.Vector([0.4, -0.4])
# Computes the transform to a rotating camera.
# --------------------------------------------
camera_rotation_radius = 6.0
# Camera rotates around the scene about 6 seconds a period.
camera_rotation_phi = frame_count / 200
# Camera looks slightly down upon the y=0 plane.
camera_rotation_theta = math.pi / 3
camera_c = camera_rotation_radius * \
ti.Vector([ti.sin(camera_rotation_theta) * ti.cos(camera_rotation_phi),
ti.cos(camera_rotation_theta),
ti.sin(camera_rotation_theta) * ti.sin(camera_rotation_phi)])
forward = ti.Vector([0.0, 1.0, 0.0], dt=ti.f32) - camera_c
up = ti.Vector([0.0, 1.0, 0.0], dt=ti.f32)
# right x up = -forward -> up x -forward = right
right = (forward.cross(up)).normalized()
up = (right.cross(forward)).normalized()
forward = forward.normalized()
camera_orientation = ti.Matrix(cols = [right, up, -forward])
kNumMSAA = 16
kMSAASide = 4
for (i, j) in pixels:
bg_color = ti.Vector([0.2, 0.2, 0.2])
radiance_sum = ti.Vector([0.0, 0.0, 0.0])
for oi in range(kNumMSAA):
offset = [(oi % kMSAASide) / kMSAASide + 0.5/kMSAASide,
(oi // kMSAASide) / kMSAASide + 0.5/kMSAASide]
# Computes the ray origin and dir using GLC.
near_point = ti.Vector([(i+offset[0]) * 2.0 / kWidth - 1,
(j+offset[1]) * 2.0 / kWidth - 1])
bc_coord = compute_barycentric_coord(A0, B0, C0, near_point)
far_point = A1*bc_coord[0] + B1*bc_coord[1] + C1*bc_coord[2]
ray_o = ti.Vector([near_point[0], near_point[1], 0.0])
ray_dir = ti.Vector([far_point[0] - near_point[0], far_point[1] - near_point[1], -1.0])
ray_o = (camera_orientation @ ray_o) + camera_c
ray_dir = (camera_orientation @ ray_dir).normalized()
(is_hit, radiance) = compute_radiance(ray_o, ray_dir)
if is_hit:
radiance_sum += radiance
else:
radiance_sum += bg_color
pixels[i, j] = radiance_sum / kNumMSAA
gui = ti.GUI("General Linear Camera", res=(kWidth, kHeight))
print('>> pixels[0, 0] = ', pixels[0,0])
for i in range(800):
paint(i)
gui.set_image(pixels.to_numpy())
gui.show()