import numpy as np
import taichi as ti
ti.init(arch=ti.gpu)
# dimension of simulation system
DIM = 3
WINDOW_SIZE = 1024
rgb2hex = lambda x: x[0].astype(np.int) * 65536 + x[1].astype(np.int) * 256 + x[2].astype(np.int)
@ti.data_oriented
class MolecularDynamics:
# cutoff radius, interaction is not calculated
# if two particles are farther than cutoff
rcut = 2.5
ecut = 4. * (1. / rcut ** 12 - 1. / rcut ** 6)
# thermostat "damping" coefficients
Q1 = 5
Q2 = 5
'''
Initializes the object, set up python scope
variables and taichi vectors.
'''
def __init__(self, density, temperature, boxlength, dt=5e-3):
# python scope variables
self.rho = density
self.boxlength = boxlength
self.dt = dt
self.n_particles = int(density * boxlength ** DIM)
# ti variables
self.position = ti.Vector(DIM, dt=ti.f32, shape=self.n_particles)
self.velocity = ti.Vector(DIM, dt=ti.f32, shape=self.n_particles)
self.force = ti.Vector(DIM, dt=ti.f32, shape=self.n_particles)
# kinetic energy
self.ek = ti.var(dt=ti.f32, shape=())
# potential energy
self.ep = ti.var(dt=ti.f32, shape=())
# temperature
self.temp = ti.var(dt=ti.f32, shape=())
# initialize system
self.init_thermostat()
self.init_pos()
self.init_velocity()
self.temp.fill(temperature)
# spawns GUI
self.gui = ti.GUI("MD", res=WINDOW_SIZE)
def set_temp(self, temperature):
self.temp.fill(temperature)
'''
Initializes the simulation system. Place particles on a regular grid
and randomize their velocities according to the temperature. Also
initializes the thermostat.
'''
def init_pos(self):
n_pow = int(self.n_particles ** (1. / DIM))
# n_axes = [nx, ny, ...] is the number of particles along each axis to be placed.
n_axes = np.array([n_pow] * DIM)
for i in range(DIM):
if n_pow ** (DIM - i) * (n_pow + 1) * i < self.n_particles:
n_axes[i] += 1
disp = self.boxlength / n_axes
coords_1d = [d * (0.5 + np.arange(n)) for d, n in zip(disp, n_axes)]
self.position.from_numpy(
np.stack(np.meshgrid(*coords_1d)).reshape(DIM, -1)[:, :self.n_particles].T)
def init_velocity(self):
vs = np.random.random((self.n_particles, DIM)) - 0.5
vcm = np.mean(vs, axis=0).reshape((1, DIM))
vs -= vcm
vs *= np.sqrt(DIM * self.temp[None] * self.n_particles / np.sum(vs ** 2))
self.velocity.from_numpy(vs)
def init_thermostat(self):
self.xi = ti.var(dt=ti.f32, shape=2)
self.vxi = ti.var(dt=ti.f32, shape=2)
self.xi.fill(0)
self.vxi.fill(0)
'''
Calculates distance with periodic boundary conditions
and wraps a particle into the simulation box.
'''
@ti.func
def calc_distance(self, x1, x2):
dist = ti.Vector([0.0] * DIM)
for i in ti.static(range(DIM)):
dist[i] = x1[i] - x2[i]
if dist[i] <= -0.5 * self.boxlength:
dist[i] += self.boxlength
elif dist[i] > 0.5 * self.boxlength:
dist[i] -= self.boxlength
return dist
@ti.func
def wrap(self, x):
for i in ti.static(range(DIM)):
if x[i] <= 0:
x[i] += self.boxlength
elif x[i] > self.boxlength:
x[i] -= self.boxlength
return x
'''
Calculates the interaction energy between two particles.
'''
@ti.func
def interaction_energy(self, r2):
return 4. * (1. / r2 ** 6 - 1. / r2 ** 3) - self.ecut
'''
Calculates magnitude of the force between two particles
multipiled by their distance.
'''
@ti.func
def force_times_dist(self, r2):
return 24. * (2. / r2 ** 6 - 1. / r2 ** 3)
'''
Substeps to integrate the thermostat.
'''
@ti.func
def step_vxi1(self, G1):
self.vxi[0] *= ti.exp(-self.vxi[1] * self.dt * 0.125)
self.vxi[0] += G1 * self.dt * 0.25
self.vxi[0] *= ti.exp(-self.vxi[1] * self.dt * 0.125)
@ti.func
def step_vxi2(self, G2):
self.vxi[1] = self.vxi[1] + G2 * self.dt * 0.25
@ti.func
def step_xi(self):
self.xi[0] += self.vxi[0] * self.dt * 0.5
self.xi[1] += self.vxi[1] * self.dt * 0.5
'''
Integrate the thermostat by half a time step.
'''
@ti.kernel
def integrate_thermostat(self):
G2 = self.Q1 * self.vxi[0] ** 2 - self.temp[None]
self.step_vxi2(G2)
G1 = (2 * self.ek[None] - 3 * self.n_particles * self.temp[None]) / self.Q1
self.step_vxi1(G1)
self.step_xi()
s = ti.exp(-self.vxi[0] * self.dt * 0.5)
self.ek[None] *= s * s
G1 = (2 * self.ek[None] - 3 * self.n_particles * self.temp[None]) / self.Q1
self.step_vxi1(G1)
G2 = (self.Q1 * self.vxi[0] ** 2 - self.temp[None]) / self.Q2
self.step_vxi2(G2)
for i in self.velocity:
self.velocity[i] = self.velocity[i] * s
'''
Integrate the motion of particles. Use Newton'w law of motion and
verlet integration scheme. Also calculates the kinetic and potential energies.
'''
@ti.kernel
def integrate_motion(self):
self.ek[None] = 0.0
self.ep[None] = 0.0
for i in self.position:
self.position[i] = self.wrap(self.position[i] \
+ self.velocity[i] * self.dt * 0.5)
self.force[i].fill(0)
for i, j in ti.ndrange(self.n_particles, self.n_particles):
if i < j:
d = self.calc_distance(self.position[i], self.position[j])
r2 = (d ** 2).sum()
if r2 < self.rcut ** 2:
rf_norm = self.force_times_dist(r2)
# += performs atomic add
self.force[i] += rf_norm * d / r2
self.force[j] -= rf_norm * d / r2
self.ep[None] += self.interaction_energy(r2)
for i in self.position:
self.velocity[i] = self.velocity[i] + self.force[i] * self.dt
self.ek[None] += (self.velocity[i] ** 2).sum() / 2
self.position[i] = self.wrap(self.position[i] \
+ self.velocity[i] * self.dt * 0.5)
'''
Renders a simulation frame to the GUI.
'''
def render(self, savefile=None):
camera = self.boxlength
radius = 8
bg = np.array([17, 47, 65])
circ = np.array([122, 200, 225])
self.gui.clear(rgb2hex(bg))
while self.gui.get_event(ti.GUI.PRESS):
if self.gui.event.key == ti.GUI.ESCAPE:
exit()
if self.gui.event.key == ti.GUI.UP:
self.temp[None] = round(self.temp[None] + 0.1, 1)
if self.gui.event.key == ti.GUI.DOWN:
if self.temp[None] <= 0.15:
self.temp[None] /= 2
else:
self.temp[None] = round(self.temp[None] - 0.1, 1)
xy = self.position.to_numpy()
z = xy[:, 2]
xy = xy[:, :2]
z_order = np.argsort(z)[::-1]
sizes = radius * camera / (camera + z)
z = (1 - z / np.max(z))
colors = rgb2hex(np.outer(bg, 1 - z) + np.outer(circ, z))
t_actual = 2 * self.ek[None] / (self.n_particles * DIM)
color_t = 0xf56060 if abs(t_actual - self.temp[None]) > 0.02 else 0x74e662
self.gui.circles(xy / self.boxlength, radius=sizes[z_order], color=colors[z_order])
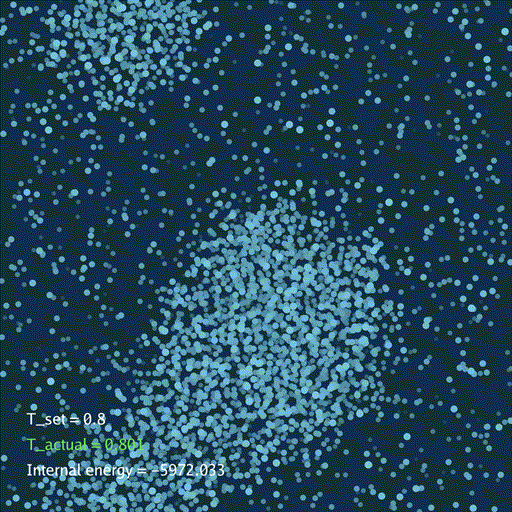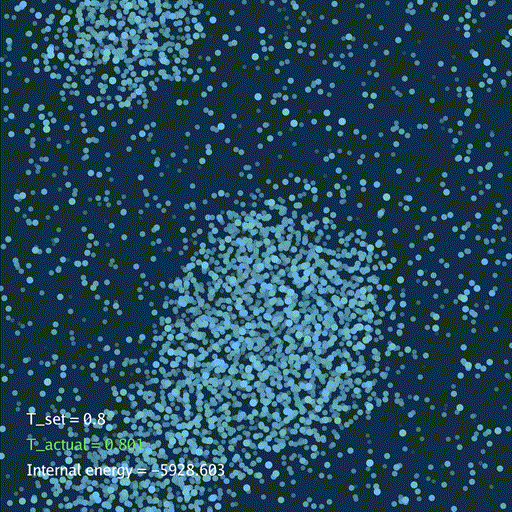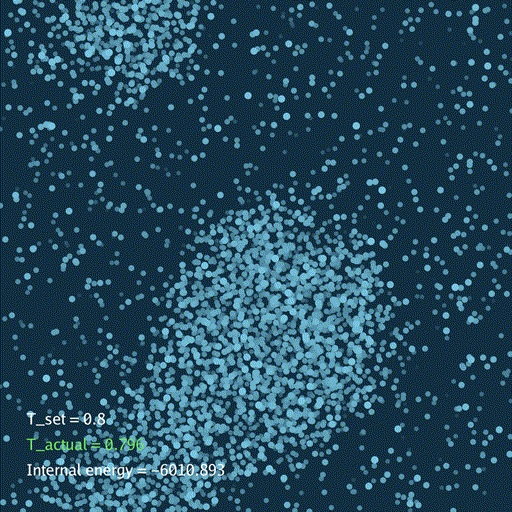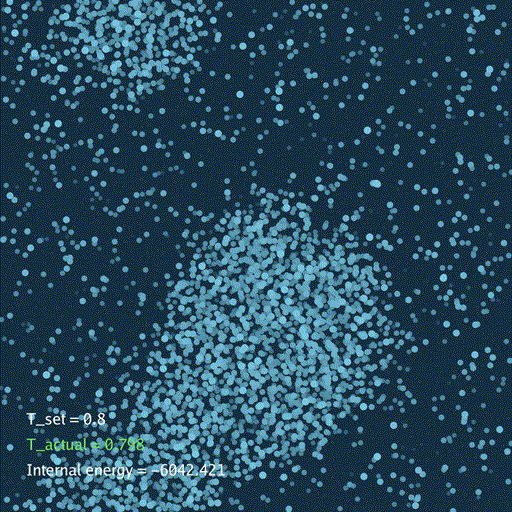
self.gui.text("T_set = %.3g" % self.temp[None], (0.05, 0.2), font_size=36)
self.gui.text("T_actual = %.3g" % t_actual, (0.05, 0.15), font_size=36, color=color_t)
self.gui.text("Internal energy = %.3f" % (self.ek[None] + self.ep[None]), (0.05, 0.1), font_size=36)
self.gui.show(savefile)
'''
Runs the simulation.
'''
def run(self, time, irender=10, save=False):
nframe = int(time / self.dt)
for i in range(nframe):
self.integrate_thermostat()
self.integrate_motion()
self.integrate_thermostat()
if irender > 0 and i > 0 and i % irender == 0:
if save:
self.render("frame%i.png" % i)
else:
self.render()
if __name__ == "__main__":
# number of particles
n = 4000
density = 0.1
temperature = 0.5
boxlength = (n / density) ** (1 / DIM)
md = MolecularDynamics(density, temperature, boxlength)
print(md.n_particles, boxlength)
# initially run a few steps at a high temperature
# to randomize the structure
md.set_temp(1.5)
md.run(md.dt * 5000, irender=-1)
md.set_temp(temperature)
# Press UP to increase the temperature and press DOWN to decrease
md.run(1e8)
分子动力学模拟(MD)通过牛顿运动定律计算微观体系中原子和分子的运动轨迹。和弹簧质点体系一样,都是求解运动方程对时间的积分。分子动力学一般使用显式的Verlet积分法, 除了计算粒子的速度和位置以外,为了在恒定温度下进行模拟还需要引入一组附加量,其作用是改变粒子的速度(Nose–Hoover thermostat).