实现了简单的3d sph
简单移植了一下SPlisHSPlasH中的代码,使用了它的核函数
近邻查找也用了最简单的网格法,实际上还可以优化到hash
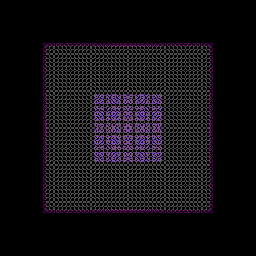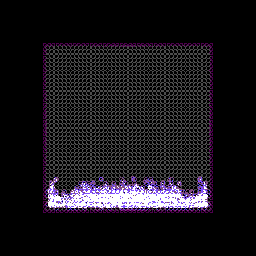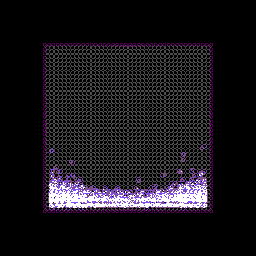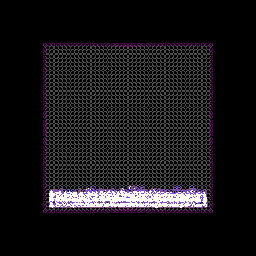
下图是近邻查找的示意图,使用正交投影,灰色和蓝色的圆圈代表了一个立方体grid,如果grid中
有粒子,那么这个grid被涂成蓝色,否则是灰色,粉色是边界条件固体粒子,白色是液体粒子:
下图是对pcisph的实现,使用了透视视角:

实现了简单的3d sph
简单移植了一下SPlisHSPlasH中的代码,使用了它的核函数
近邻查找也用了最简单的网格法,实际上还可以优化到hash
下图是近邻查找的示意图,使用正交投影,灰色和蓝色的圆圈代表了一个立方体grid,如果grid中
有粒子,那么这个grid被涂成蓝色,否则是灰色,粉色是边界条件固体粒子,白色是液体粒子:

下图是对pcisph的实现,使用了透视视角:

好消息:
1.实现了iisph
2.修复了近邻中,有一个边界粒子没有赋值的bug
3.修复了sesph和pcisph中没有使用volume估计,只用中心点的bug
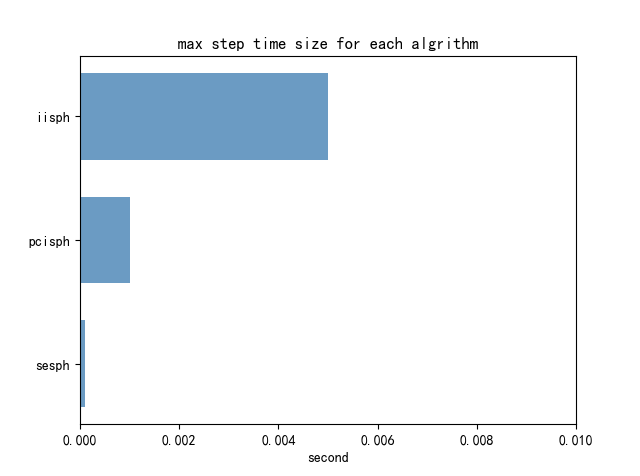
下图是三种sph方法的最大时间步长比较
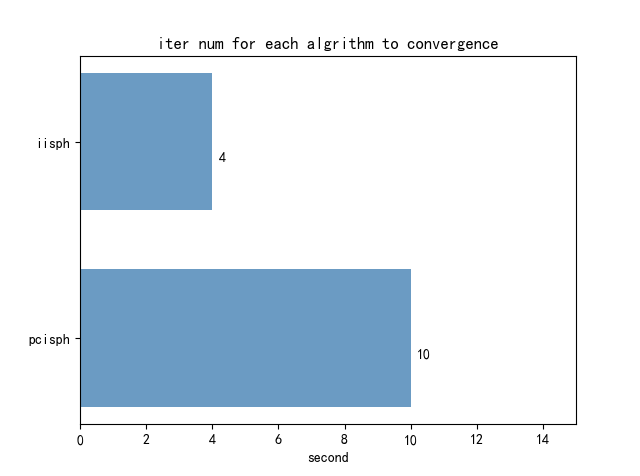
下图是对比iisph和pcisph两种方法的迭代次数
最后上两张粘性比较的gif,均使用iisph:


future work:
1.想研究下2019年的bender的volume maps方法,这样边界做起来更加简单,但恐怕能力不够,读不懂paper
2.marching cube使用taichi实现,将sph的grid输出,使用marching cube重建,或者看看pcl和openvdb看看python调用能不能实现
3.particle raytrace,不构建表面的情况下,实现渲染,Direct Raytracing of Particle-based Fluid Surfaces Using Anisotropic Kernels,这篇mark一下
在实现任意mesh的边界条件时,发现2019年的那篇有点难涉及到mesh转sdf,gpu kdtree等技术,退而求其次,实现2012年那篇简单的。
1.实现了泊松圆盘采样在任意的obj模型上:

使用了gpu排序,减少了cpu到gpu数据拷入拷出的时间,复杂度log(n)*log(n)*n
2.将其和iisph合体,做了一个效果,液体特别黏才能稳定,即使我在SPlisHSPlasH也试了一下,没法再这个边界条件下稳定住,还是得再探索下

more work:
实现下高级的粘性和涡度,还是参照SPlisHSPlasH里面的论文去研读
把固体边界的粘性系数和液体粘性系数分开计算,重新绘制了一张图

新功能实现:
[1] 实现了M Weiler 2018: A physically consistent implicit viscosity solver for SPH fluids
超粘的液体

粘到像砖头一样

[2]用precondition cg 求解了粘性加速度,过程是matrix free的
之前课程中踢到有一个教程关于conjugate gradient的无痛教程:
我找到了一个中文版本的,感谢翻译君:
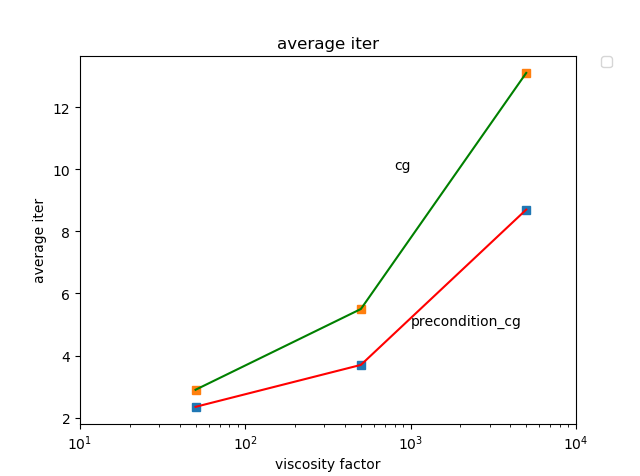
对比一下不使用预处理cg和precondition cg之间的迭代效率
[3] 近邻搜索网格已经更新成hashmap,由之前的空间复杂度 o(n3),变为o(m), n是整个场景aabb切分成小立方体,m是粒子数量
future work:
[1] mesh to sdf算法研究, 液体粒子可以以任意形状产生,然后为volume map做铺垫
[2] compact hash研究 提升缓存命中率
我找到一本包括了CG, CGS, BiCG, BiCGSTAB各种算法和预处理的书,里面提供了很不错的伪代码。书名叫做" Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods"。处于版权关系就不在这里放链接了。。
新功能:
[1] 重构了下代码,hashmap和camera分开,做了两个动画

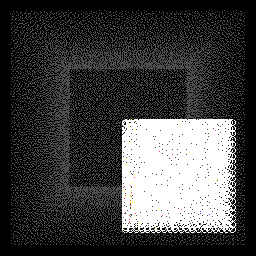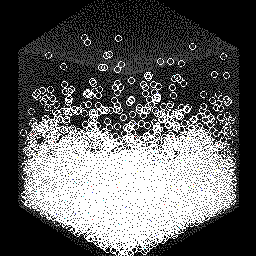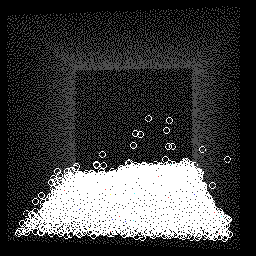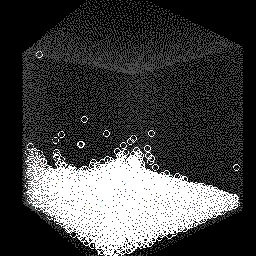
[2]实现了dfsph,时间步长相比iisph增大5倍
[3]实现了tension和vorticity,暂时没找到合适的三维模型用于演示
[4]实现了CFL可变时间步长,写了一个并行统计最大速度的kernel
[5]修复了一些bug,特别是boundry handle里面改用了 Geodesic Distance而不是直接距离
计划做一下:
[1] foam generation
[2] particle rendering


左边是marching cube
右边参考了TOG的一篇论文做的平滑
该论文被用在了flex和physX5.0中
请问下是弱可压sph吗,用在工程仿真准确度如何呀?
恩,是的。但sph应用一般只有影视游戏,追求视觉效果类似,工程上,你可以看看fluent软件,据我所知,FEM数值正确性更强,大学时候同学写毕设用过,看起来很专业的样子 
嗯嗯是的,但是SPH在CFD领域用的也很多,我同门就是用SPH搞CFD,但是我看和图形学的SPH并没有本质区别甚至图形学会用到更多数据结构和优化方法,所以除了CFD的工程应用时候的SPH考虑了更多细节和边界条件外,我真没看出有很大差别,因为图形学的sph忽略掉的细节想加上也很容易
SPH在CFD领域主要用于不可压缩流的模拟,细分的话主要集中在自由面流和多相流。但是有利有弊吧,入口边界和出口边界条件就是一大难题。但是这些在动画里都不会考虑。粒子的领域搜索、排序等数据接口可以借鉴,但是和工程应用相比,还是有很大不同